Vortex Methods
Introduction
The present research focuses on the developmemt of mesh-free vortex methods, capable of solving high Reynolds number flows with an accuracy and speed comparable to that of grid based direct numerical simulations.
The vortex method is volume-mesh-free, meaning that it only requires a mesh at the wall or interface. It expresses the flow field by a superposition of finitesimal vortex elements, and has an advantage in solving high Reynolds number flows with complex geometries and moving boundaries.
The favorable features of this method can be summerized as follows
- It treats convection in a Lagrangian manner, and thus, is immune to the problem between numerical stability and artificial diffusion.
- Acceleration algorithms inherent to particle methods (Tree code, Fast Multipole Method), and also the special purpose computers designed to accelerate the N-body calculation (GRAPE, MD-GRAPE)are exploitable in the vortex method.
- The calculation points are automatically concentrated to the region of large gradients, so the distribution of calculation points is consistently optimized.
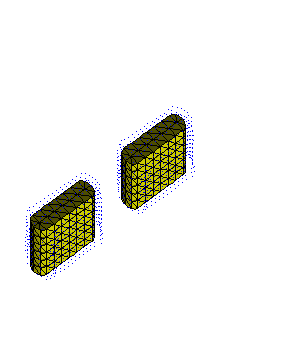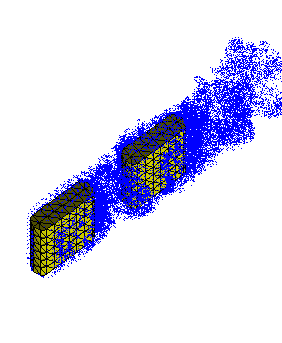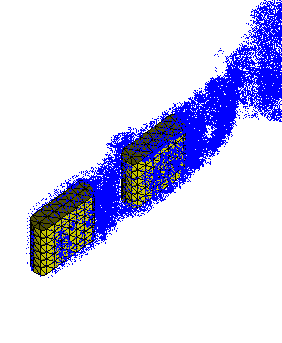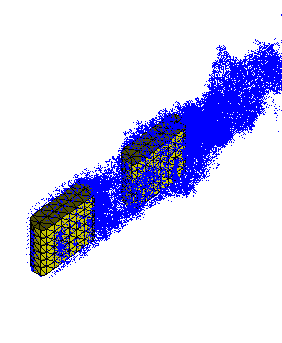
The above figure shows the convection of vortex elements in blue, around two tandem bluff bodies discretized using 2nd order triangular elements shown in yellow. The blue vortex elements are created from each of these yellow triangular panels every few time steps. This is a rather crude example of the vortex method calculation, where the spatial resolution is insufficient and the particle distortion is not compensated for.
Flow fields like the one shown above, have many different sources of errors for vortex methods. We have isolated some of these errors by comparing with DNS results in canonical turbulence.

The above figures are the isosurface of the second invariant of the velocity gradient tensor. The right is the result of the pseudo-spectral method, and the left shows the result of the vortex method calculation. The calculations are for a decaying homogeneous isotropic turbulence with an initial Taylor's microscale Reynolds number of 25. The number of calculation points was N=64^3. There are no obvious differences in the plots.
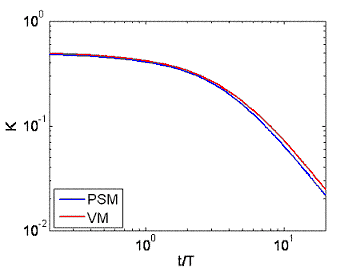
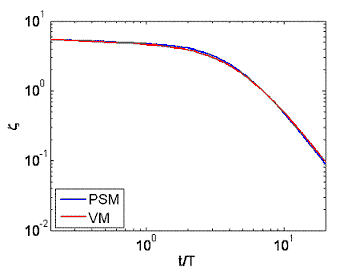
The above figures show the decay of kinetic energy and enstrophy in the isotropic turbuelnce calculation. The right is the kinetic energy and the left is the enstrophy. The PSM and VM are the results of the pseudo-spectral method and vortex method, respectively. The time is normalized by the eddy turnover time. The results indicate that the decay of kinetic energy in 3-D isotropic turbulence can be calculated accurately. Thus, the viscous diffusion alone is no longer a problem for vortex methods.
Peer-reviewed journal publications
- Yokota, R. and Obi, S., Comparing vortex methods and finite difference methods in a homogeneous shear flow, Int. J. for Numerical Methods in Fluids, 63-7, 828-846, 2010. doi:10.1002/fld.2102
- Yokota, R., Narumi, T., Sakamaki, R., Kameoka, S., Obi, S., Yasuoka, K., Fast Multipole Methods on a Cluster of GPUs for the Meshless Simulation of Turbulence, Computer Physics Communications, 180-11, 2066-2078, 2009. doi:10.1016/j.cpc.2009.06.009
- Sheel, T. K., Yokota, R., Yasuoka, K., and Obi, S., The study of colliding vortex rings using a special-purpose computer and FMM, Transactions of the Japan Society for Computational Engineering and Science, 20080003, 2008.
- Yokota, R., Sheel, T. K., and Obi, S., Calculation of isotropic turbulence using a pure Lagrangian vortex method, Journal of Computational Physics, 226-2, 1589-1606, 2007. doi:10.1016/j.jcp.2007.06.003
- Sheel, T. K., Yasuoka, K., and Obi, S., Fast vortex method calculation using a special-purpose computer; Computers and Fluids, 36-8, 1319-1326, 2007. doi:10.1016/j.compfluid.2007.01.006
- Totsuka, Y. and Obi, S., A validation of viscous dissipation models for fast vortex methods in simulations of decaying turbulence, Journal of Fluid Science and Technology, 2-1, 248-257, 2007.
- Totsuka, Y. and Obi, S., Viscous dissipation models for the fast vortex calculation of decaying turbulence, Transactions of the Japan Society of Mechanical Engineering B 71-701, 23-29, 2005.
Conference presentations
- R. Yokota, K. Fukagata, and S. Obi, Lagrangian Vortex Methods in Turbulent Channel Flows, 12th EUROMECH European Turbulence Conference, 2009/9/7-10
- R. Yokota and S. Obi, Validation of Vortex Methods in a Turblent Channel Flow, Annual meeting of the JSFM, Tokyo, Japan, 2009/9/2-4
- R. Yokota, T. Narumi, R. Sakamaki, K. Yasuoka, and S. Obi, Fast Multipole Methods on GPUs for the Meshfree Simulation of Turbulence, 10th US National Congress on Computational Mechanics, 2009/7/16-19
- R. Yokota, T. Narumi, R. Sakamaki, S. Kameoka, K. Yasuoka, and S. Obi, DNS of Homogeneous Turbulence Using Vortex Methods Accelerated by the FMM on a Cluster of GPUs, 21st International Conference on Parallel Compuational Fluid Dynamics, USA, 2009/5/18-22
- R. Yokota, T. Narumi, R. Sakamaki, S. Kameoka, K. Yasuoka, and S. Obi, Meshfree Simulation of Turbulence Using the Fast Multipole Methods on GPUs, 22nd Symposium on Computational Fluid Dynamics, Tokyo, Japan, 2008/12/17-19
- R. Yokota, S. Obi, Vortex Method Simulation of Turbulent Channel Flow, Annual meeting of the JSFM, Kobe, Japan, 2008/9/7
- R. Yokota, S. Obi, Direct numerical simulation of homogeneous shear flow using vortex methods, 4th International Conference on Vortex Flows and Vortex Models, Seoul, Korea, 2008/4/21-23
- T. K. Sheel, R. Yokota, K. Yasuoka, and S. Obi, Calculation of the decay of colliding turbulent vortex rings, 4th International Conference on Vortex Flows and Vortex Models, Seoul, Korea, 2008/4/21-23
- R. Yokota, S. Obi, Mesh-free simulation of the homogeneous shear flow using vortex methods, 23rd IIS Turbulence and Shear Flow Dynamics Symposium, Tokyo, Japan, 2008/3/7
- A. Sato, R. Yokota, and S. Obi, Computation of wing-tip vortex by a three-dimensional vortex method, 21st Symposium on Computational Fluid Dynamics, Tokyo, Japan, 2007/12/19-21
- R. Yokota, T. Narumi, K. Yasuoka, T. Ebisuzaki, and S. Obi, Mesh-free direct numerical simulation of turbulence using the vortex method on parallel MDGRAPE-3 boards along with the fast multipole method, Next-Generation Supercomputing Symposium, Tokyo, Japan, 2007/10/3-4
- R. Yokota, S. Obi, Pure Lagrangian vortex methods for the simulation of decaying isotropic turbulence, 5th International Symposium on Turbulence and Shear Flow Phenomena, Munich, Germany, 2007/8/27-29
- R. Yokota, S. Obi, Vortex methods for the calculation of homogeneous shear flows, Annual meeting of the JSFM, Tokyo, Japan, 2007/8/6-8
- T. K. Sheel, K. Yasuoka, and S. Obi; Acceleration of vortex method calculation using a special-purpose computer and FMM, International Conference on Computational Methods, Hiroshima, Japan, 2007/4/4-6
- R. Yokota, S. Obi, Mesh-free turbulence simulation using vortex methods, 56th Conference of the JSME Tokai Branch, Hamamatsu, Japan, 2007/3/7-8
- R. Yokota, S. Obi, Simulation of homogeneous isotropic turbulence using the vortex method, 20th Symposium on Computational Fluid Dynamics, Nagoya, Japan, 2006/12/18-20
- R. Yokota, S. Obi, Calculation of fluid structure interaction using VEM and BEM, Conference of the JSME Fluid Engineering Division, Kawagoe, Japan, 2006/10/28-29
- R. Yokota, S. Obi, Simulation of a wake using a 3-D vortex element method, Annual Meeting of the JSME, Kumamoto, Japan, 2006/9/18-22
- R.Yokota, S.Obi, Vortex flow simulation of between multiple bridge decks, Whither Turbulence Prediction and Control, Korea, 2006/3/29
- R. Yokota, S. Obi, Vortex flow simulation of multipole bluff bodies, 19th Symposium on Computational Fluid Dynamics, Tokyo, Japan, 2005/12/13-15
- R.Yokota, S.Obi, Vortex Flow Simulation of Multiple Bluff Bodies, The Third International Conference on Vortex Flows and Vortex Models, Yokohama, Japan, 2005/11/22
- T.K.Sheel, K. Yasuoka, and S.Obi, Acceleration of Vortex Method Calculation using MDGRAPE-2: A special-purpose computer, The Third International Conference on Vortex Flows and Vortex Models, Japan, 2005/11/22
- R. Yokota, N. Tokai, and S. Obi, Vortex flow simulation of multipole bluff bodies, 17th Conference on Computational Mechanics, Sendai, Japan, 2004/11/18-20
- Y. Totsuka, S. Obi, The Vortex Method Applied to Simulation of Homogeneous Isotropic Turbulence, International Conference on Computational Methods, Singapore, FP212, 2004/12/15
- Y. Totsuka, S. Obi, Analysis of the Homogeneous Isotropic Turbulence by a Three Dimensional Vortex Element Method, Proceedings of the Second International Conference on Vortex Methods, Istanbul, Turkey, 2001/9/27
